A decorator is a Python function that takes a function object as an argument and returns a function as a value. Here is an example of decorator definition:

1
2
3
4
5
6

def foo(function):
    # make a new function
    def new_function():
        # some code

    return new_function

To apply a decorator to an existing function, you just need to put @decorator_name in the line before its definition, like this example:

1
2
3

@foo
def hello():
    print 'Hello World'

This decorator doesn’t do anything, so let’s think about a more concrete problem we could solve using decorators.

Fibonacci sequence

By definition, the first two numbers in the Fibonacci sequence are either 1 and 1 or 0 and 1. All the other numbers are the sum of the previous two numbers of the sequence. Example:

1. 0, 1: the third number is 1
2. 0, 1, 1: the fourth number is 2
3. 0, 1, 1, 2: the fifth number is 3
4. 0, 1, 1, 2, 3: the sixth number is 5
5. etc…

If we wanted to give a math definition of the sequence, we could describe it in this way:

• F(0): 0
• F(1): 1
• F(n): F(n-1) + F(n-2)

In Python we could have a recursive function like the following one:

1
2
3
4
5

def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)

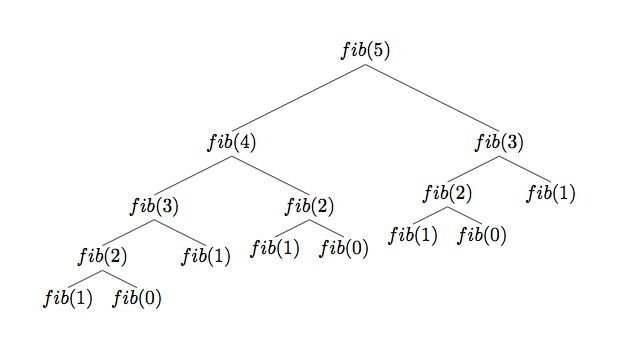
What’s the problem with this implementation? The code works as expected, but it’s very inefficient. The next picture will explain what happens when we will try, for example, to calculate the 5th number of the sequence:

{ width=60%}

Fib(5) is Fib(4) + Fib(3), but Fib(4) itself is Fib(3) + Fib(2), and… the picture just tell us that we have calculated Fib(3) 2 times, Fib(2) 3 times, Fib(1) 5 times! Why are we repeating the same operation every time if we already calculated the result?

Memoization

In computing, memoization is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again.

We need to store values of the sequence we have already calculated and get them later when we need them. Let’s implement a simple memoization decorator:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def memoize(function):
    cache = {}

    def decorated_function(*args):
        if args in cache:
            return cache[args]
        else:
            val = function(*args)
            cache[args] = val
            return val
    return decorated_function

The decorator defines a dict at the beginning that is used as a cache. When we want to find the n number of the sequence, it first checks if the value was already calculated and that value is returned instead of being calculated again. If the value is not found, then the original function is being called and then the value is store in the cache, then returned to the caller.

Using the memoize decorator

How much this decorator can speed up our fib method? Let’s try to benchmark the execution using Python timeit module.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

# First example, not using the memoize decorator

import timeit

def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)

t1 = timeit.Timer("fib(35)", "from __main__ import fib")
print t1.timeit(1)

The required time to calculate the 35th number of the Fibonacci sequence on my laptop is: 4.73480010033

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# Second example, using the memoize decorator

import timeit
from memoize import memoize  # For convenience I put my decorator
                            # in a module named memoize.py

@memoize
def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)

t1 = timeit.Timer("fib(35)", "from __main__ import fib")
print t1.timeit(1)

The required time to calculate the 35th number of the Fibonacci sequence on my laptop is: 0.000133037567139

Quite faster, don’t you think? I will let you try how long does it take to calculate the 60th number of the sequence with and without using the decorator. Hint: grab a cup of coffee before beginning!